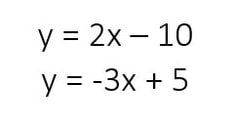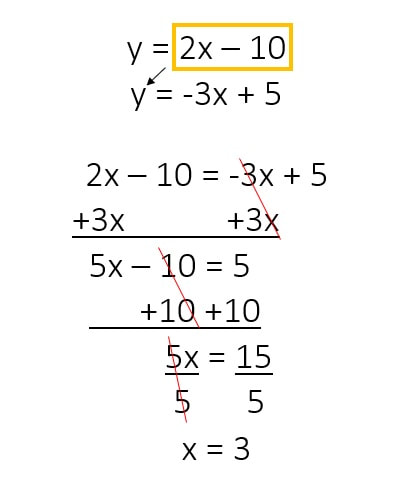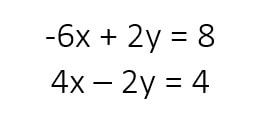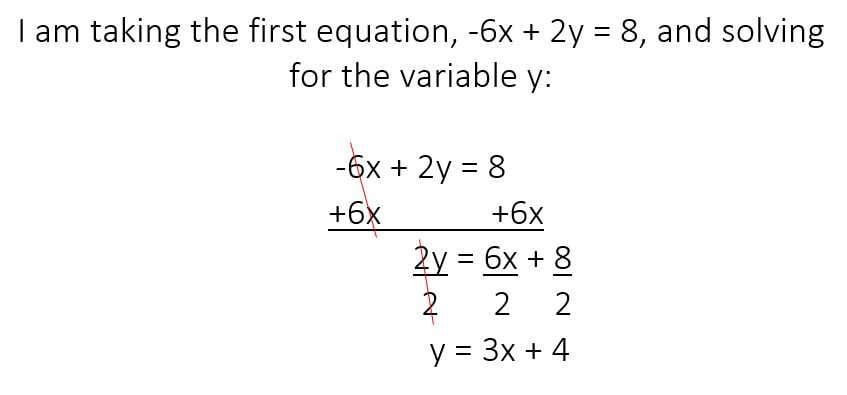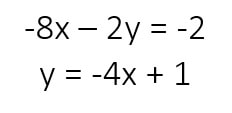How do we solve a systems of equations by substitution?
We can solve a systems of equations using substitution by isolating a variable in one of the given equations and plugging it into the other given equation.
As seen earlier, there are 3 types of solutions.  When solving the systems of equations, there will either be one solution, no solutions, or infinitely many solutions.
Now in order to solve a system of equations by substitution, it is best to have one of the variables isolated so that we can plug it into the other equation.

​Let's look at some examples:

Example #1

Solve the systems of equations by substitution:
The first thing that I notice from the system of equations is that both equations are in slope-intercept form
(y is solved for in both equations).  This means that I can go straight into plugging in the value of one of the variables into the other equation.

Example #2

Solve the systems of equations by substitution:
Now, in this systems of equations I notice that both equations do not have a variable isolated.  I can decide if I would want to isolate either the x or y variable, and I can decide to isolate the variable in either equation.  I am just going to choose to isolate y in the first equation.  You should get the same answer regardless if you decided to isolate x, or isolated a variable in the second equation.

Practice

Solve the following systems of equations by substitution:
Click here to check your answer.