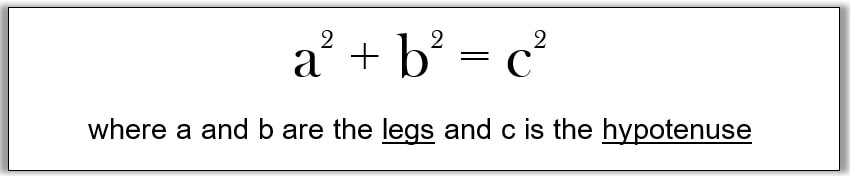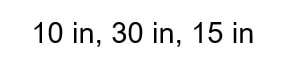Objectives:
  • Define the Pythagorean Theorem
  • Use the Pythagorean Theorem to find a missing length in a right triangle
  • Use the Converse of the Pythagorean Theorem to determine if a triangle is a right triangle

What is the Pythagorean Theorem?

The Pythagorean Theorem states that given a right triangle, the length of the longest side of the triangle when squared is equal to the sum of the other lengths when squared.  In other words,
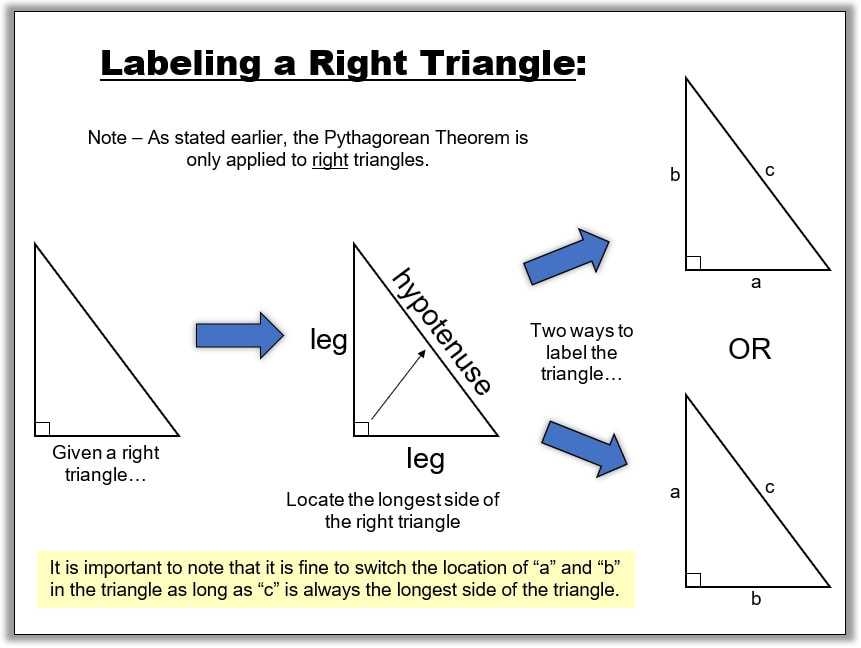
Given a right triangle, we will denote the longest side of the triangle as "c". This is also known as the hypotenuse. If we have trouble determining the longest side of the triangle, we can look at the right angle and go to the side that is "across" from it. This will always be the longest side of the right triangle. The other sides of the right triangle are called the "legs" and are denoted as "a" and "b".

Let's look at a picture:
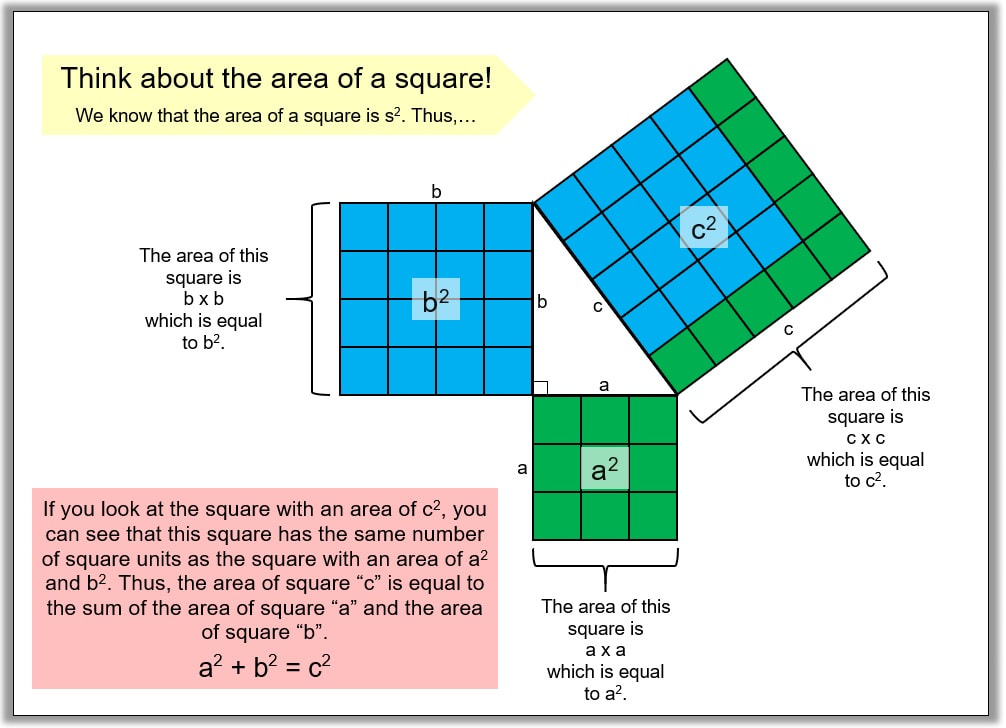
Now, let's look at how the Pythagorean Theorem was derived:

Examples

Now that we know about the Pythagorean Theorem and how it was derived, we can look at some problems!

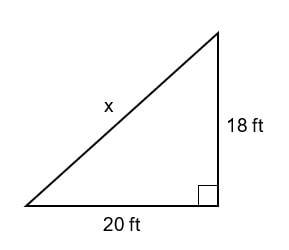
Your Turn #1

Given the right triangle below, solve for x:
Click HERE to check your answer.
In the previous example, the missing length was the hypotenuse. Let's look at an example where we are given the hypotenuse.

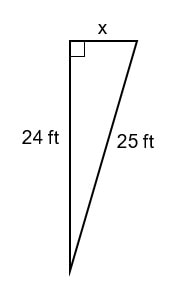
Your Turn #2

Given the right triangle below, solve for x:
Click HERE to check your answer.

The Converse of the Pythagorean Theorem

We have learned how to use the Pythagorean to find a missing length in a right triangle. However, what if we are given all lengths of the triangle and need to find out if it forms a right triangle? This is called the Converse of the Pythagorean Theorem! Let's look at some examples!

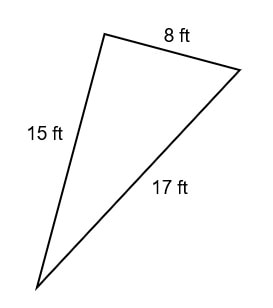
Your Turn #3

Determine if the following triangle is a right triangle:
Click HERE to check your answer

Your Turn #4

Determine if the following side measurements form a right triangle:
Click HERE to check your answer.

Quiz

You will take the quiz after you have researched and taken notes on the Pythagorean Theorem.
​CLICK HERE FOR QUIZ