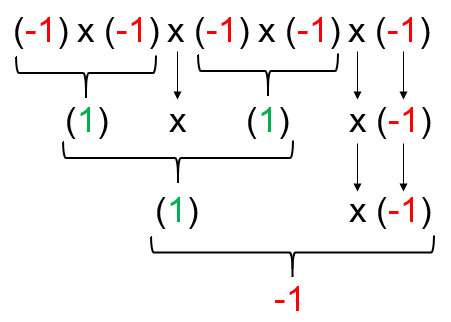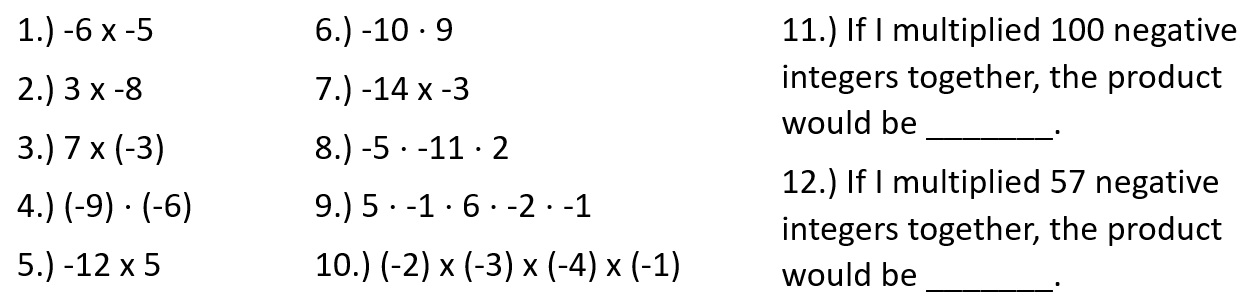Objectives:
- Determine the product of two or more integers.
Multiplying Integers using Rules
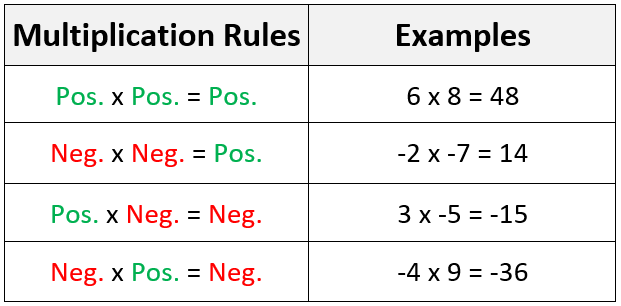
We can multiply integers by using the multiplication rules. These rules are:
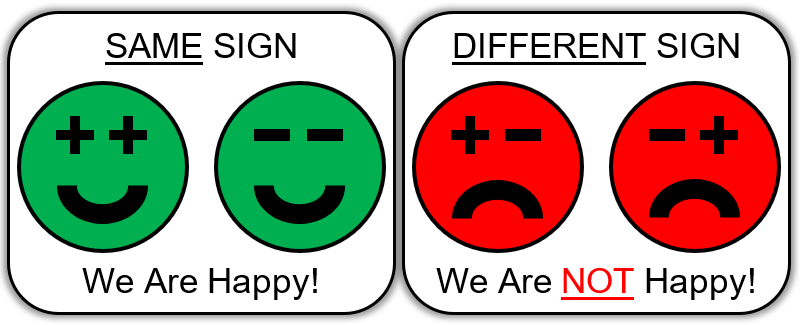
The image below is a way that can help us remember the multiplication rules.
When the sign is the same, we are happy! If the signs are different, we are NOT happy!
When the sign is the same, we are happy! If the signs are different, we are NOT happy!
Now, what if we multiply multiple integers together? For example, what if I multiplied a positive number of integers together. For example, if I multiple the following 4 negative integers together...
(-1) x (-1) x (-1) x (-1)
Would the product be positive or negative?
What about if I multiplied a negative number of integers together, For example, if I multiple the following 5 negative integers together...
(-1) x (-1) x (-1) x (-1) x (-1)
Would the product be positive or negative?
Lets explore this below!
(-1) x (-1) x (-1) x (-1)
Would the product be positive or negative?
What about if I multiplied a negative number of integers together, For example, if I multiple the following 5 negative integers together...
(-1) x (-1) x (-1) x (-1) x (-1)
Would the product be positive or negative?
Lets explore this below!
Multiplying Multiple Integers
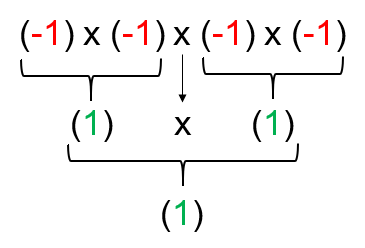
First, lets look at the product of 4 negative integers.
From earlier, we know that the product of two negatives is positive. We can apply this knowledge when multiplying multiple integers together. So,
From above, we can see that the product of 4 negatives is positive.
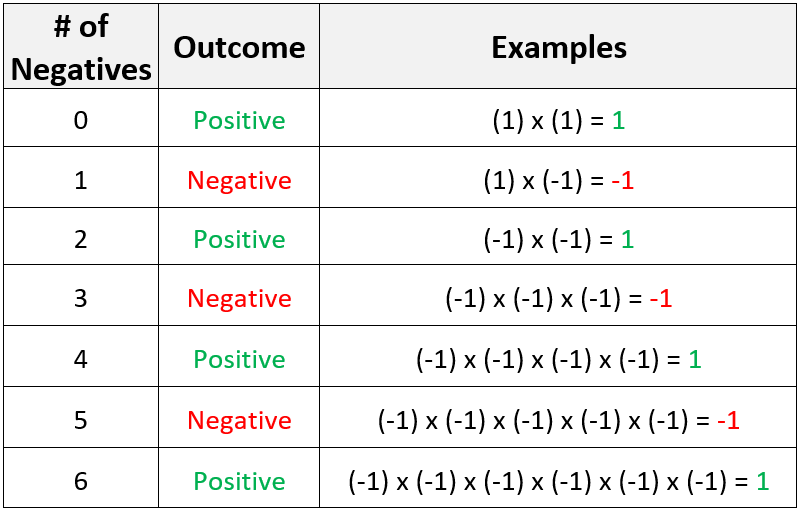
This shows us that if we have an even amount of negatives then the product will always be positive.
This shows us that if we have an even amount of negatives then the product will always be positive.
Lets take a look at another example. Lets consider the product of 5 negative integers. If we apply the multiplication rules from above, we can see that...
From above, we can see that the product of 5 negatives is negative.
This shows us that if we have an odd amount of negatives then the product will always be negative.
This shows us that if we have an odd amount of negatives then the product will always be negative.
The table below shows us that there is a pattern when multiplying by a certain amount of negative integers.
We can see that if we are given a positive number of negatives then the product will be positive. If we are given a negative number of negatives then the product will be negative.
Examples
Determine the product of the following:
Click HERE to check your answers
Quiz
(C) 2017 MATH IN DEMAND