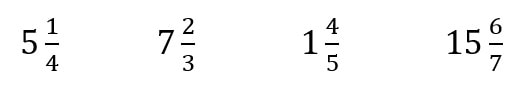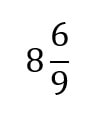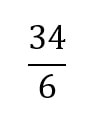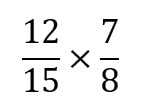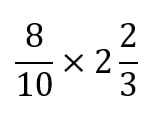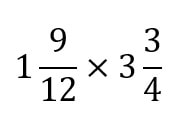Multiplying Fractions

Objectives:

Convert a mixed number into an improper fraction, and vice versa.
Determine the product of two fractions.
Reduce or simplify a fraction to its lowest terms.

What is a mixed number?
A mixed number is a whole number with a fraction. Some examples include:

What is an improper fraction?
An improper fraction is a fraction that has a numerator that is greater than the denominator. Some examples include:

Converting a Mixed Number into an Improper Fraction:

Before we get into multiplying fractions, we need to learn how to convert a mixed number into an improper fraction. When multiplying fractions, we do not want to have a mixed number. So let's look at an example:

Example #1

Your turn! Convert the following mixed number into an improper fraction:

Click HERE to check your answer.

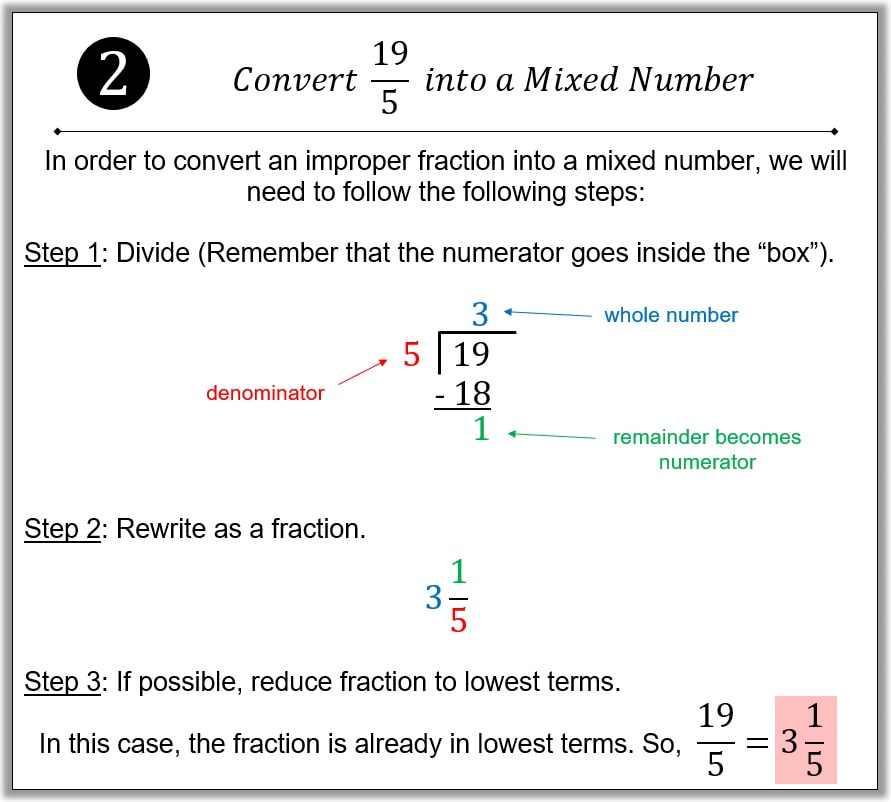
Converting an Improper Fraction into a Mixed Number:

Last piece of information that we need to know before we can multiply fractions is how to convert an improper fraction into a mixed number. The reason why we need to know this is because the product of some fractions may end up being improper fractions. We don't want to leave our answers in improper fractions. Hence, we will need to convert our answers into mixed numbers. Let's look at an example:

Example #2

Your turn! Convert the following improper fraction into a mixed number:

Click HERE to check your answer.

Multiplying Fractions

Now that we have went over how to convert mixed numbers into improper fractions (and vice versa), we are ready to multiply fractions! It is important to know that when we multiple fractions, we multiply "across". This is NOT the same as "cross multiplication". Let's look at a few examples: