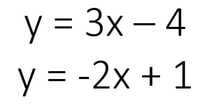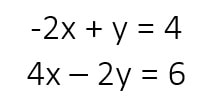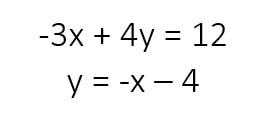How do we solve a systems of equations by graphing?
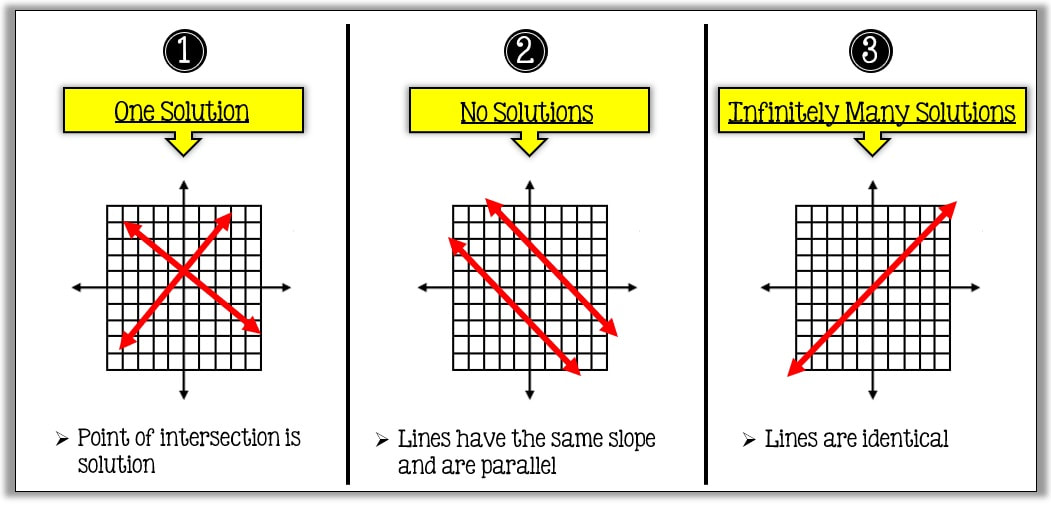
We can solve a systems of equations by graphing each linear equation on the same graph.  The point of intersection between the two graphs is the solution.
As seen earlier, there are 3 types of solutions.  When graphing the systems of equations, they will either have one solution, no solutions, or infinitely many solutions.
Now in order to graph the linear equations, we want the equations to be in slope-intercept form.  This means that we want "y" to be solved in each equation. Once each equation is in slope-intercept form (y = mx + b), then we can graph the equations and identify the solution(s).

​Let's look at some examples:

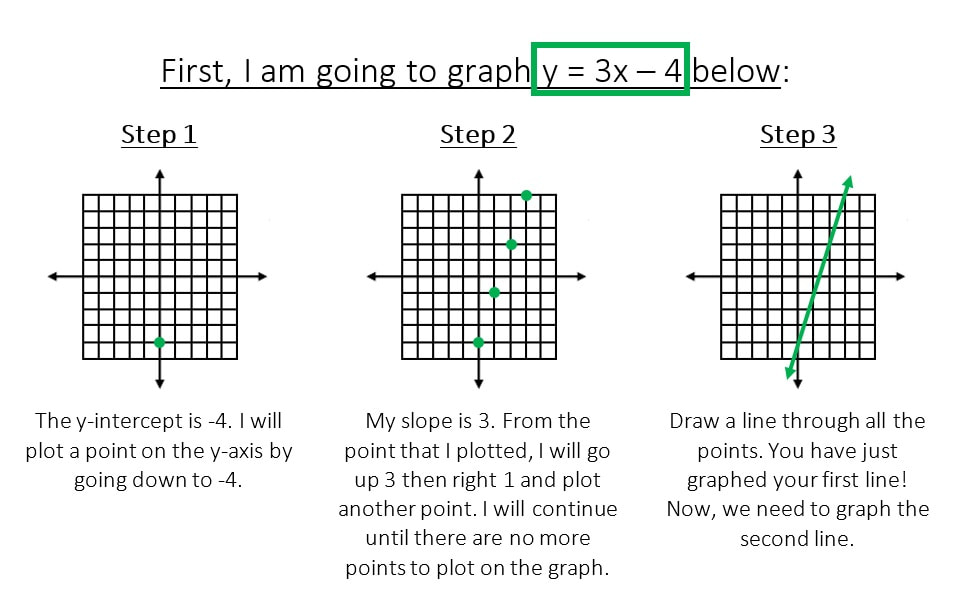
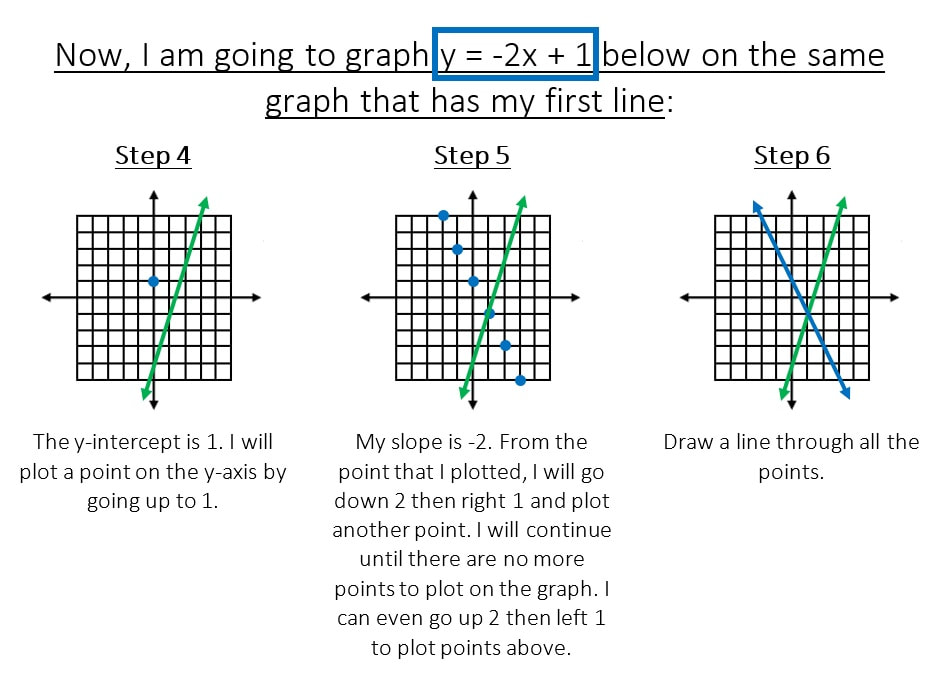
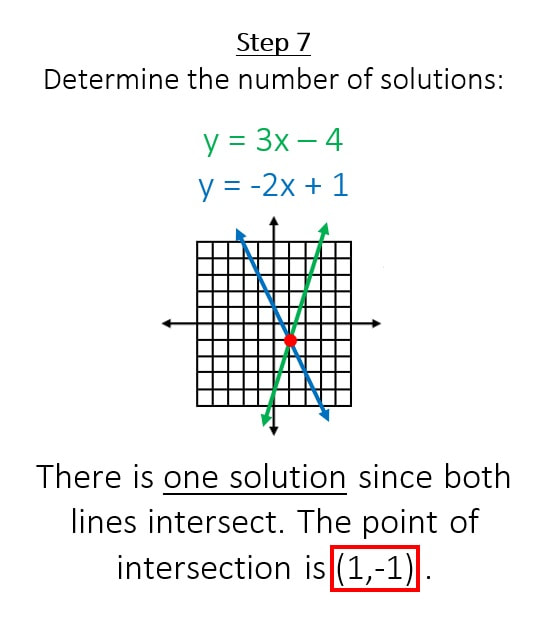
Example #1

Solve the systems of equations by graphing:
The first thing that I notice from the system of equations is that both equations are in slope-intercept form
(y is solved for in both equations).  This means that I can go straight to graphing each equation.

Example #2

Solve the systems of equations by graphing:
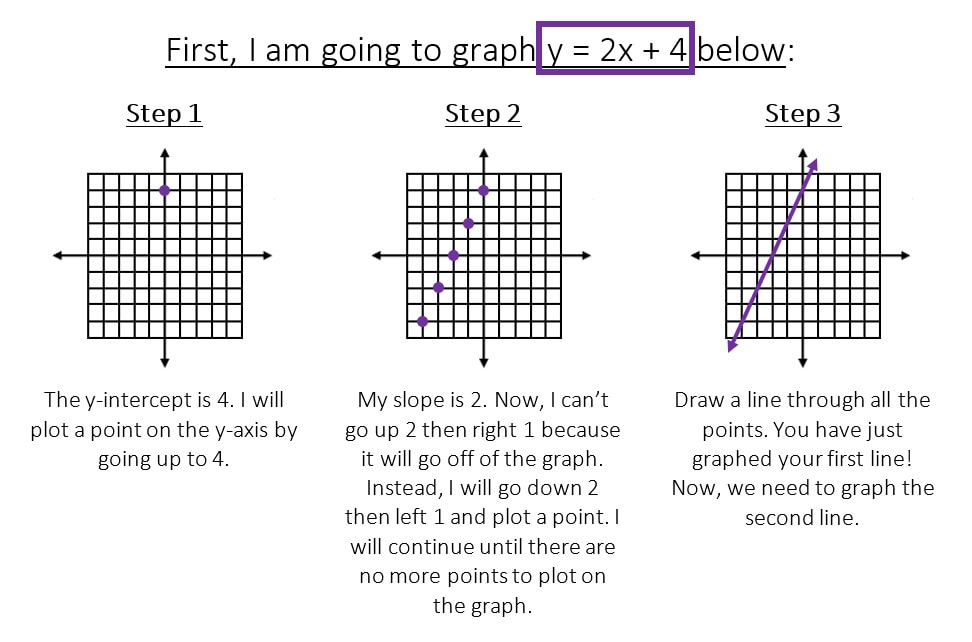
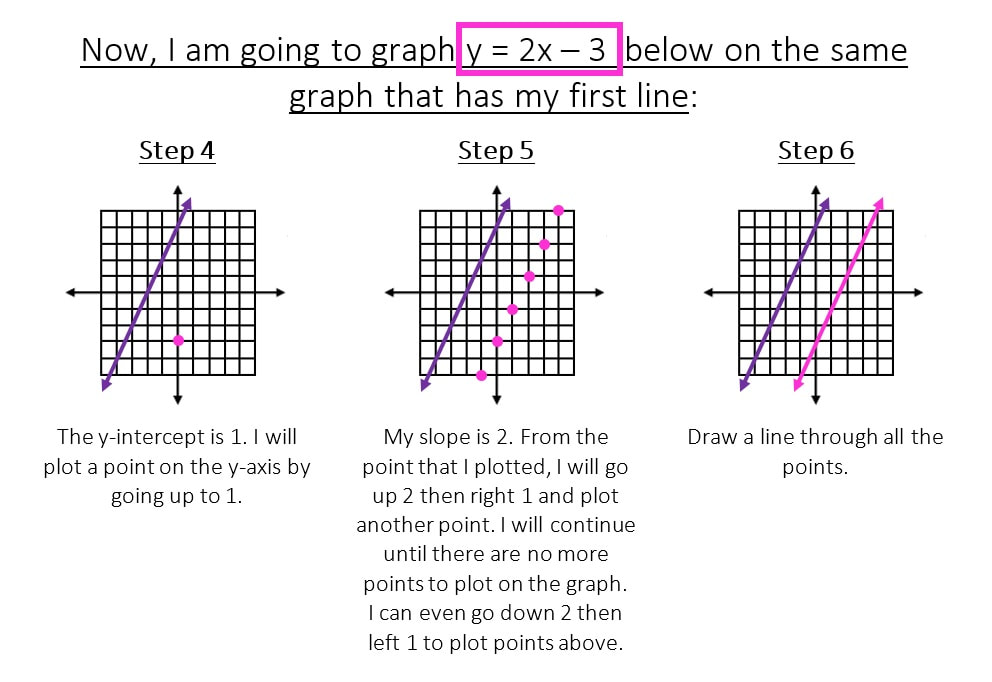
Now, in this systems of equations I notice that both equations are NOT in slope-intercept form (y is not solved for in both equations).  This means that I need to solve for y in each equation before I can graph the system of equations.

Practice

Solve the following systems of equations by graphing:
Click here to check your answer.