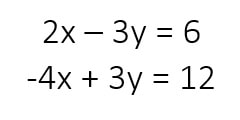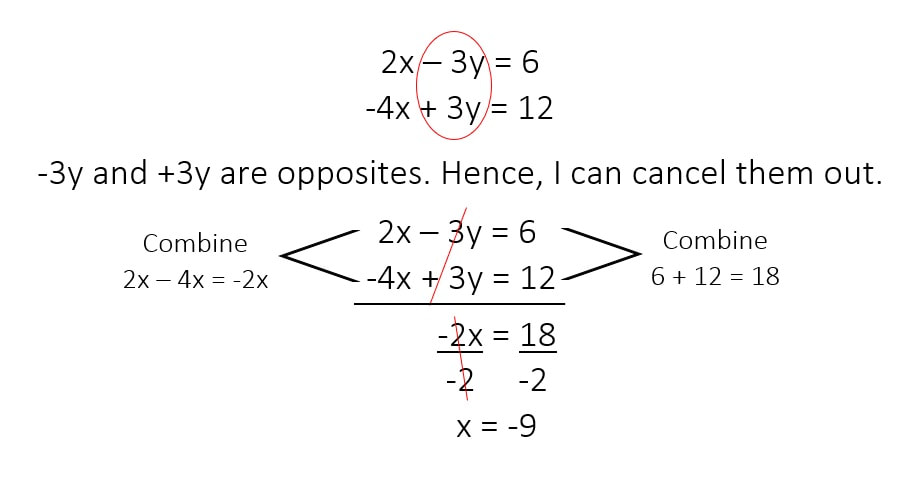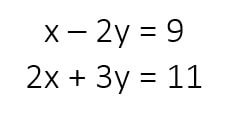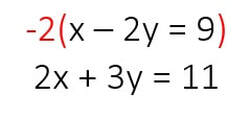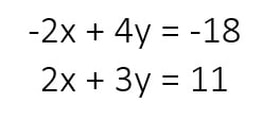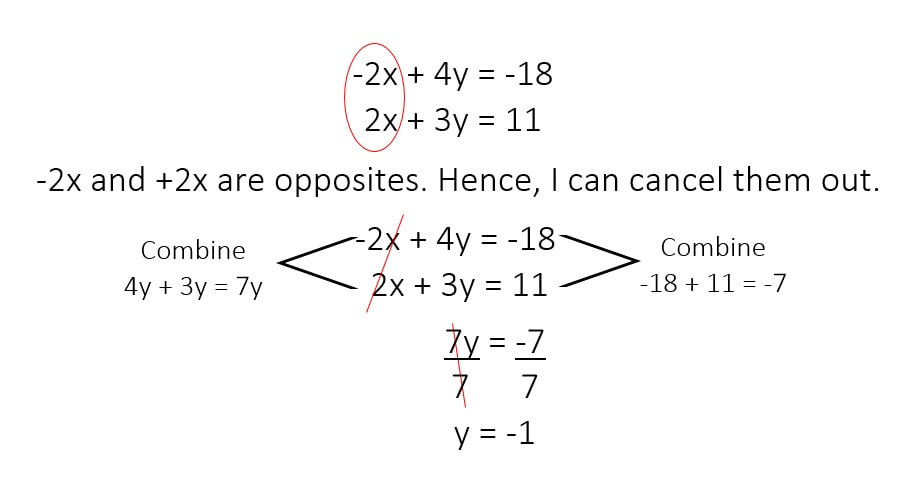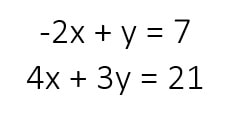How do we solve a systems of equations by elimination?
We can solve a systems of equations using elimination by "getting rid" of one variable then solving for the other variable.
As seen earlier, there are 3 types of solutions.  When solving the systems of equations, there will either be one solution, no solutions, or infinitely many solutions.
Now in order to solve a system of equations by elimination, we need to have "opposites" for one of the variables.  For example, given the following system of equations:

 4x - 2y = 6
-4x + 4y = 8

We can see that 4x and -4x are "opposites" and cancel out.  This would allow us to solve for y.  Yet, you will see some systems of equations were there are no opposites.  In this case, you would need to either multiple one of the equations or both of the equations by a factor so that you can make opposites. 

​Let's look at some examples where we solve the system of equations by using elimination:

Example #1

Solve the systems of equations by elimination:
The first thing that I notice from the system of equations is that I can cancel out the variable y because -3y and +3y are opposites.  This will allow me to solve for x:

Example #2

Solve the systems of equations by elimination:
Now, in this systems of equations I notice that there are no opposites for either variable.  This means that I need to multiple either one or both equations to make opposites.  I can see that if I multiple the entire first equation by -2 then I will have opposites for my x variable:
After multiplying the entire first equation by -2, we get:

Practice

Solve the following systems of equations by elimination:
Click here to check your answer.