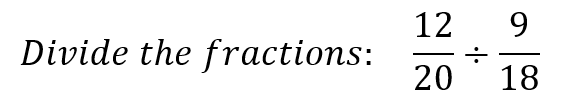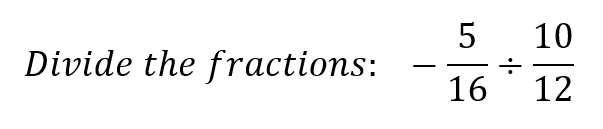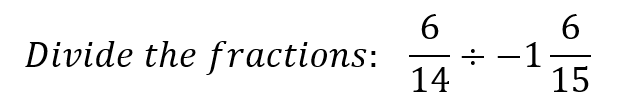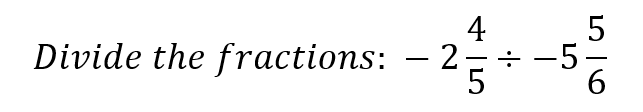Objectives:
- Convert a mixed number into an improper fraction, and vice versa.
- Determine the quotient of two fractions (where the fractions can be negative).
- Reduce or simplify a fraction to its lowest terms.
In the previous lesson, you learned how to multiply two fractions including negative fractions. You will see that we can change any division problem into a multiplication problem by making two changes. The 2 changes are...
(1) - Take the reciprocal of the second fraction (the second fraction is the divisor)
Reciprocal means to "flip" the fraction so that the numerator becomes the denominator and the denominator becomes the numerator). Let's look at 3 examples...
(1) - Take the reciprocal of the second fraction (the second fraction is the divisor)
Reciprocal means to "flip" the fraction so that the numerator becomes the denominator and the denominator becomes the numerator). Let's look at 3 examples...
(2) Change the division sign into a multiplication sign.
After you make these changes, you can multiply the fractions as you have previously learned!
After you make these changes, you can multiply the fractions as you have previously learned!
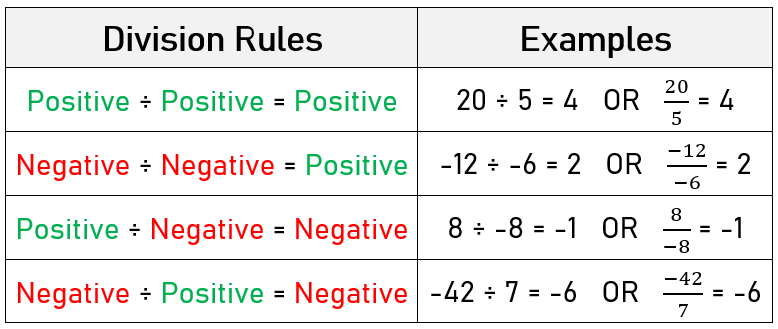
Before we begin dividing fractions, do you remember the division rules for integers? If not, let's refresh our minds:
Division Rules
These rules also apply when we are dividing fractions. Thus, these rules will come in handy for the next
4 examples. Let's take a look below!
4 examples. Let's take a look below!
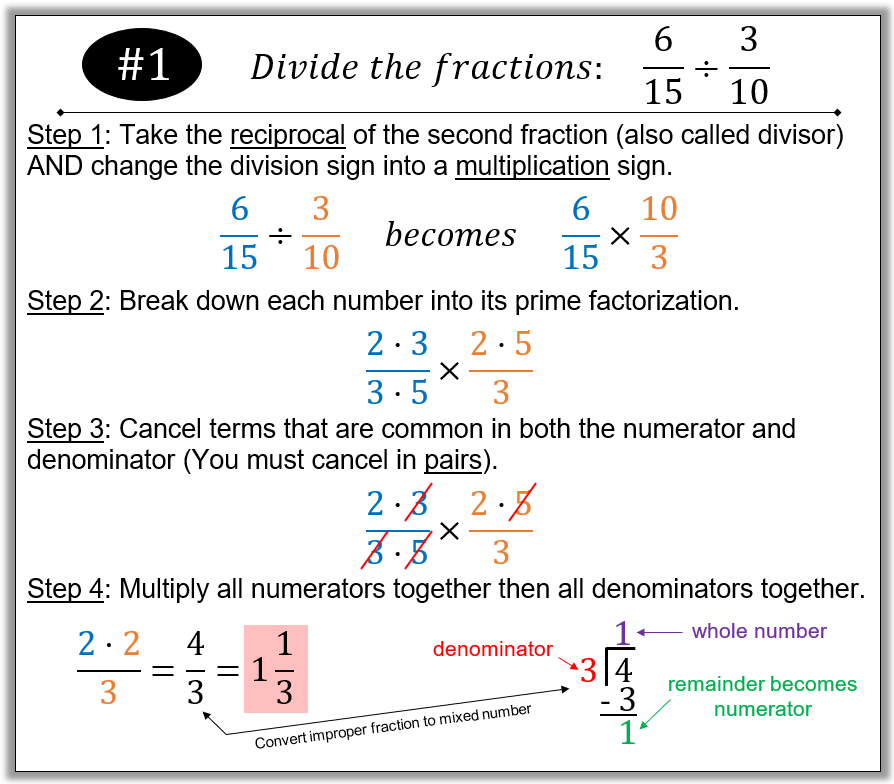
Example #1
The Quotient of Two Positive Fractions
Your Turn #1
Click HERE to check your answer.
Example #2
The Quotient of a Negative Fraction Divided by a Positive Fraction
Your Turn #2
Click HERE to check your answer.
Example #3
The Quotient of a Positive Fraction Divided by a Negative Fraction
Your Turn #3
Click HERE to check your answer.
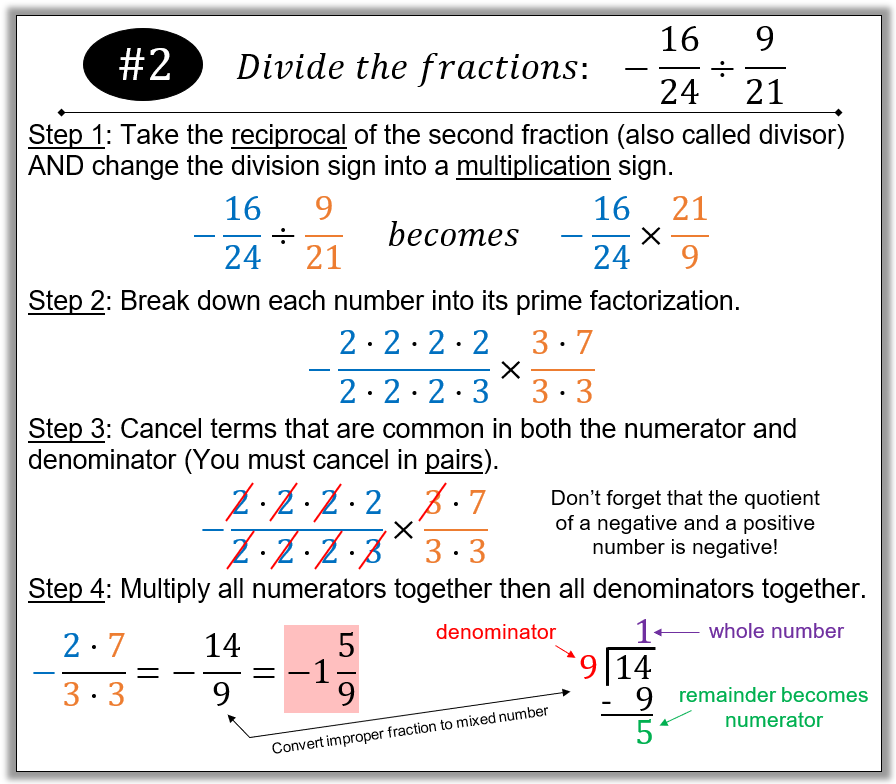
Example #4
The Quotient of Two Negative Fractions
Your Turn #4
Click HERE to check your answer.
Quiz
You will take the quiz after you have taken notes.
CLICK HERE FOR QUIZ
CLICK HERE FOR QUIZ
(C) 2017 MATH IN DEMAND